Elastizititätstheorie der Baustatik

Stand 2000

Bei einer plastischen Formänderung verläuft der Rückgang im Spannungs-Dehnungs-Diagramm auf einer Parallelen zu dem elastischen Arm.

Die Bernoulli-Hypothese, die besagt, dass die Querschnitte senkrecht auf Stabachse stehen, sie ist gültig für kleine Verformungen und sofern keine Querkraftbeanspruchung vorliegt.

Das Superpositionsprinzip besagt, dass sich bei der Überlagerung von Kräften eine Überlagerung der Schnittgrössen ergibt.

Der Gleitmodul wird mit G bezeichnet.

Das Torsionsträgheitsmoment wird mit I_T bezeichnet.

Elastische Formänderungen

Voraussetzungen für elastische Formänderungen sind die Gültigkeit der Bernoulli-Hypothese, sowie des Hookesches Gesetzes. Weiterhin müssen die Verformungen klein in Relation zu maßgeblichen Querschnittsabmessungen sein.

Aus diesen Annahmen  folgt konsequenterweise, daß eine  Linearität zwischen den Belastungen und Verformungen vorliegt und das Superpositionsprinzip gilt.

Formänderungen aufgrund elementarer Beanspruchungen

Formänderungen infolge Normalkraftbeanspruchung In einem Stab der Länge l ,der durch N beansprucht wird, wird ein differentiell kleines Teilchen der Länge dx um du verlängert.

ε = du/dx

α = N/A

Es gilt das Stoffgesetz: α = E * ε.

Daraus läßt sich eine elementare Verformungsbeziehung ableiten:

du = N / (E*A) * dx

E*A ist die sogenannte Dehnsteifigkeit oder auch Normalsteifigkeit.

Die gesamte Formänderung des Stabes ergibt sich durch Integration über seine Länge:

∫du = ∫N /(E*A) *dx = N *l / (E*A)

Formänderungen infolge Biegebeanspruchung

Die Durchbiegung wird mit w(x) bezeichnet.

Die Verdrehung wird mit ϑ bezeichnet.

Balken durch ein konstantes Moment M belastet: M wirkt somit an beiden Seiten des differentiell kleinen Teilchens. Längenänderung der Faser ist  ε(z)dx. Der Winkel dϑ ìst ungefähr gleich seinem Tangens.

&epsilon(z)dx /z = tan(dϑ)

α = M /I*z

α = E * ε

Daraus läßt sich eine elementare Verformungsbeziehung ableiten:

σ = E * dϑ * z/dx

dϑ = M /(E*I) * dx

E*I ist die sogenannte Biegesteifigkeit oder auch Momentensteifigkeit.

Analogie von Mohr

Die erste Ableitung des Biegemomentes ist die Querkraft, die zweite Ableitung des Biegemomentes ist die negative Belastung.

Die folgende Formel nutzt MathML und wird eventuell in einigen Browsern nicht korrekt dargestellt! Erfolgreich getestet mit Mozilla Firefox.

$\frac{d^{2}w}{{\mathrm{dx}}^2}=-q\left(x\right)$

Formänderungen infolge Querkraftbeanspruchung

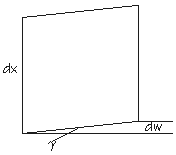
Ein einseitig eingespannter Träger wird am Ende durch F beansprucht. Ein differentiell kleines Teilchen wird somit beidseitig durch Q beansprucht. Es stellen sich Gleitungen ein. τ ist von z abhängig.Die mittlere Gleitung γ_m ist ungefähr gleich dw/dx.  Die mittlere Schubspannung τ_m ist gleich Q/A.

τ = G * γ

τ_m = 1/ κ * G * γ_m.

κ ist  ein querschnittsabhängiger Korrekturfaktor.

Daraus läßt sich eine elementare Verformungsbeziehung ableiten:

dw = Q / (G*A) * κ * dx

G*A

ist die sogenannte  Schubsteifigkeit oder auch Gleitsteifigkeit.

Formänderung infolge Torsionsmonentenwirkung.

Wird ein runder Stab mit dem Radius r durch ein Torsionsmoment M_T beansprucht, so wird auch ein differentiell kleines Teilchen im Stab beidseitig durch M_T belastet, es stellen sich Gleitungen ein. Es stellt sich eine Verdrehung, auch Torsion genannt, um den Winkel dϑ ein. Der Gleitwinkel ist γ_T.

γ*dx ist ungefähr dϑ * r

τ_T = M_T / I_T * r

τ_T= G*γ_T

Daraus läßt sich eine elementare Verformungsbeziehung ableiten:

dϑ = M_T / (G * I_T) *dx

G*I_T ist die sogenannte Torsionssteifigkeit.

Kein Moment im Feld Resultat: Keine Krümmung unbelasteter Schleppträger: Keine Schnittgrößen.

Elastizitätsforderung

Ermittlung der Einflußzahlen: z.B. Verdrehungen.

Verträglichkeitsbedingung

Auflager und Gelenke sind Unstetigkeitsstellen

Gegenseitigkeit der elastischen Formänderungen

Satz von Bett

Die Arbeit der Lastengruppe i auf den Wegen δ_k, die von der Lastengruppe k verursacht werden, ist gleich der Arbeit der Lastengruppe k auf den Wegen δ_i, die von der Lastengruppe i hervorgerufen werden.

W_ik = W_ki

Satz von Maxwell

Die Verschiebung d_nm im Punkt n infolge einer Last 1 im Punkt m ist gleich der Verschiebung δ_mn im Punkt m infolge einer Last 1 im Punkt n. Kraftangriffspunkt und Meßpunkt sind vertauschbar.

4H-NISI, äußeren Kraefte, allgemeine Biegegleichung, Arbeitssatz, Auflager, Aussparungen, Beanspruchbarkeit, Beanspruchung, begleitende Dreibein, Belastungsannahmen, Belastungsumordnungsverfahren, Bemessungswertder Einwirkungen, Bernoulli-Hypothese, Bezugsrand, Biegedrillknicken, Biegeknicken, Biegerandspannung, Biegesteifigkeit, Bredtsche Formel, Clapeyron, Dehnsteifigkeit, Dehnung, DIN 1080, Dreimomentengleichung, Drillknicken, Druckkraft, Durchbiegung, Durchlaufträger, E*A, E*I, Eigenarbeit, Einwirkungen, elastische Formänderungen, Elastizitätsforderung, erforderliche Widerstandsmoment, Eulersche Knickgleichung, F, Flächenmoment 2. Grades, Formänderungsbedingungen, Formänderungsenergie, Fremdarbeit, f_y,d,, G, G, G*A, G*IT, Gleichgewichte, Gleitmodul, Gleitsteifigkeit, Gleitungen, Grad der statischen Unbestimmtheit, i, Innere Arbeit, inneren Kräfte, IT, KGV, Kipplast, Knicklänge, Knicknachweis, Knickzahl, Kombinationswert fuer Einwirkungen, Kraftgrößen, Kraftgrößenverfahren, Mohr, Momentensteifigkeit, Normalsteifigkeit, Nullinie, PCAE-DTE, Pieper/Martens, positive Normalkraft, positive Querkraft, positives Biegemoment, PvK, Q, Reduktionssatz, Resistance, Satz von Betti, Satz von Maxwell, Schnittgrößen, Schubsteifigkeit, Sicherheitsnachweis, Stabilität, Ständige Einwirkungen, statisch unbestimmte Systeme, Stützmomente, Superpositionsprinzip, Teilsicherheitsbeiwert, Temperaturausdehnungs­koeffizient, Torsion, Torsionssteifigkeit, Torsionsträgheitsmoment, Trägheitshalbmesser, Trägheitsmoment, Veränderliche Einwirkungen, Verdrehung, Verdrillung, Verschiebungsarbeit, virtuelle Kraftgrößen, Vorzeichenregelung, w(x), Weggrößen, Widerstand, Widerstandsmoment, Zugkraft, Äußere Arbeit,