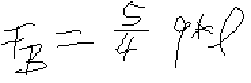Stand 2000.
plastische Formänderung: Ruckgang auf Parallele zu elastischen Gerade.
Voraussetzungen für elastische Formänderungen:
- Bernoulli-Hypothese (Querschnitte stehen senkrecht auf Stabachse) gültig für kleine Verformungen und keine Querkraftbeanspruchung vorliegt.
- Hookesches Gesetz gültig
- Verformungen klein in Relation zu maßgeblichen Querschnittabmessungen
Konsequenzen:
- Linearität zwischen Belastungen und Verformungen
- Superpositionsprinzip gilt (Bei Überlagerung von Kräften ergibt sich eine Überlagerung der Schnittgrössen)
Formänderungen elementarer Beanspruchungen
Formänderungen infolge Normalkraftbeanspruchung
In einem Stab der Länge 1 ,der durch N beansprucht wird, wird ein Teilchen mit der Länge dx um du verlängert.
ε = du/dx
σ = N/A
Stoffgesetz: σ = E *ε
=> elementare Verformungsbeziehung:
du = N / (E *A) * dx
E * A = Dehn- oder Normalsteifigkeit
int(du) = int(N/(E*A)*dx)
N *l / (E*A) = gesamte Formänderurg des Stabes
Formänderungen infolge von Biegebeanspruchung
Balken durch Konstantes Moment belastet.
Moment wirkt an beiden Seiten des differentiell kleinen Teilchens.
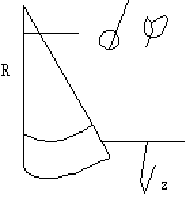
Längenänderung der Faser = ε(z)dx
dφ ist für kleine Winkel ungefähr ε(z)dx /z = tan(dφ)
σ = M/I*z
σ = E * ε
Daraus folgt: σ = E * dφ *z/dx
dφ = M/(E*I)*dx
E * I = Biege- oder Momentensteifigkeit
Formänderungen infolge von Querkraftbeanspruchungen
Einseitig eingespannter Träger wird am Ende durch F beansprucht => Teilchen beidseitig durch Q beansprucht => Gleitungen
Arbeit
Äußere Arbeit
W = F *S * cos(α)
F und S sind Vektoren, α ist der eingeschlossene Winkel.
Eigenarbeit
Eigenarbeit ist immer positiv.
Durch Fi ergibt sich die Verformung δii
- Das erste i beschreibt den Ort.
- Das zweite i beschreibt die Ursache.
int(dW)= int(Fi * δii)
Bei dynamischen Kräfte ist die Beanspruchung doppelt so groß.
Für statische Kräfte steigt die Kraft linear an.
Verschiebungsarbeit
Verschiebungsarbeit wird auch Fremdarbeit genannt.
W = Fi * δij
Ein differentiell kleines Teilchen der Länge dx wird durch N beansprucht Resultat: Verlängerung um du.
dWi = 1/2 * N * du
dWi = 1/2 * N * ε * dx
Mit Dehnungssteifigkeit:
dWi = 1/2 * N2/(E*A) * dx
Für Biegebeanspruchung:
dWi = 1/2 * M2/(E*I) * dx
Für Querkraftbeanspruchung:
dWi = 1/2 * κ * Q2/(G*A) * dx
Für Torsionsmomenterbeanspruchung:
dWi = 1/2 * MT2/(G*IT) * dx
Einzelne Arbeitsterme dürfen in der linearen Statik addiert werden.
Bei überwiegend biegebeanspruchten Systemen ist es ausreichend den Biegemomententerm zu betrachten.
Wi = int(dWi)= int(1/2*N2/(E*A)*dx)
Wi = 1/2 * N2 / (E *A) W * l
Stablänge l
Arbeitssatz
Die Äußere Arbeit ist gleich der Formänderungsenergie.
Ein Stab der Länge l verlängert sich aufgrund des Angriffes von F um u.
Wa = 1/2 * F * u
Wi = 1/2 * N2 * l / (E*A)
Wa = Wi
Die Grenzen des einfachen Arbeitssatzes:
- Berechnung von Verformungen, die nicht im Term Wa auftauchen.
- Berechnung Wi = Wii + Wij:
Wa= 1/2 * Fi * wij + 1/2 Fj * wjj + Fi * wij
Beispiel Arbeitssatz
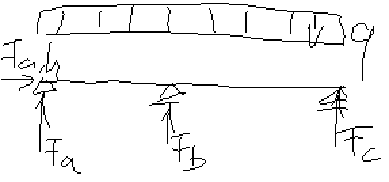
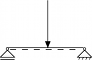
Ein Einfeldträger mit Einzellast in Feldmitte. Gesucht ist die Maximalverformung w.
Wa = 1/2 * F * w (Eigenarbeit von F)
Das System ist überwiegend biegebeansprucht. Die Wirkung von Q wird vernachlässigt.
dWi = 1/2 * M2 / (E*I) * dx
max M = F * l/4
Der Verlauf ist linear:
M(x)= F * x/2
Wi = F2/(4 * E * I) * l3/3
w = F*l3 / (48 * E * I)
Stabverdrehung
Eine Stabverdrehung kommt zustande wenn zwei gleich große Kräfte entgegengesetzt gerichtet wirken.
Die Kräfte haben einen Abstand a und greifen an einem starren Körper an.
Wa ist immer Null bei translatorischer Verschiebung.
Bei einer Rotation um M ergibt sich der Drehwinkel φ.
Für kleine Winkel δ
s = s2 - s1 = φ * a
Wa = F * φ * a = M * φ
Beispiel Stabverdrehung
Es soll die Stabverdrehung φB am freien Ende eines Kragarms unter der Wirkung eines Einzelmomentes MB am freien Ende bestimmt werden. Die Stablänge ist l.
φB ist der Winkel zwischen den Tangenten an die Biegelinie im verformten/unverformten Zustand. Das System ist überwiegend biegebeansprucht.
Momenten-Zustandslinie:
M(x)= const = MB
E*I = const
Wa = 1/2 * MB *φB
Durch Wa = Wi:
φB = MB * l / (E*I)
Das Prinzip der virtuellen Kräfte
- Durch eine virtuelle Kraft vom Betrag 1 ergibt sich eine Verformung uquer. (virtuelle Stabkräfte S1quer und S2quer
- Angriff von F. Resultat: Horizontale und vertikale Verformung. Resultierende StabKräfte S1 + S1quer und S2 + S2quer
Wa= 1/2 *1 * uquer + 1/2 F * v + 1* u
Bei Fachwerkstäben:
Ai = 1/2 * Sum(i=1, n; Si2 *li / (E*Ai))
Nach Elimination der Eigenlasten ergibt sich:
1*u = sum(i=1; n; Siquer * Si * li/(E*Ai)
Mohrsches Verfahren
DGL der elastischen Biegelinie:
w''(x) = -M(x)/(E*I)
Analogie M und w, Q und φ
Vorgehensweise
Ermittlung M(x) aus q(x)
M(x) wird als äußere Belastung q(x) aufgefaßt
Für q(x) werden die Auflagerkräfte und Querkraft deutschq(x) und Momentenflächen deutschM(x) bestimmt<
Durchbiegungen und Verformangen werden aus φ(x)= deutschq(x)/(E*I) und w(x)= deutschM(x)/(E*I) ermittelt<
Stabilität gerader Stäbe
Formen des Stabilitätsversagens
- Biegedrillknicken (auch Kippen)
- Biegeknicken
- Drillknicken
Durch Knicken gerät der Querschnitt in die Nachbarlage. Bei doppelt symmetrischen Querschnitten ergibt sich niemals eine Verdrillung.
Eulerfälle:
- einseitig fest eingespannt
- einwertig und zweiwertig gelagert; Resultat: Sinnshalbwelle
- dreiwertig und einwertig
- dreitwertig und dreiwertig
Stahl unter Druckspannung
Eulerfall II
Voraussetzungen:
- Bernoullihypothese gültig
- Hooke'sche Gesetz gültig
- Kleine Verformungen
Ist der Nachbarzustand als Gleichgewichtszustand möglich?
sum(M<sub> i(s)</sub>) = O
N * w(x) - M(x) = O
Mit DGL der elast. Biegelinie:
w''(x) + N/(E*I) * w(x) = 0
lineare DGL 2. Ordnung, homogener Bauart
Ansatz: w(x)= A*?
A = offene Konstante, Amplitude
w''(x) = -π2 / l2 * A * sin(π/l*x)
Lösung der DGL:
- A = O triviale Lösung, keine Auslenkung
- Nki = π2 * E * I / l2
Die Eulersche Knicklast, eine offene Konstante bleibt unbestimmt (Eisenwertproblem)
Trägheitsradius i = root(I/A)
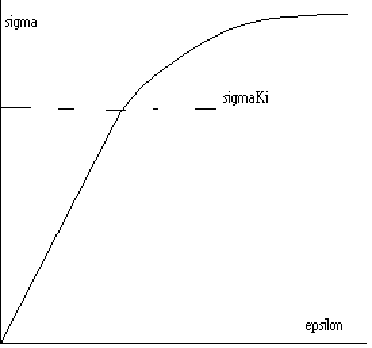
σki = π2 * E *i2 / l2
σki = π2*E / φ2
φ - Schlankheit
Eulerhyperbel
Versuch mit nachkritischem Verhalten
sk Knicklänge
sk = β * l
β = Knicklängenbeiwert
l = Netzlänge, Auflagerabstand
Nki = π2 * E *I / sk2
Eulerfall 1: β = 2
Eulerfall 2: β = 1
Eulerfall 3: β = 0,7
Eulerfall 4: β = 0,5
Nki,y Knicken um die y-Achse, Knicken in andere Richtung.
EBaustahl = 21000 kN/cm
Einteilige Druckstäbe im Holzbau unter mittigem Kraftangriff
σw = ω * N/A < zul σd
ω = Erhöhungsfaktor
ω ist näherungsweise 1 + c * (λ / λg)2
σw fiktive Druckspannung
Zulässige Schlankheiten
λ < 150 einteilige Stäbe, Starrachse mehrteilger Stäbe
λ < 175 für die nachgiebige Achse von mehrteiligen Stäben
DIN 1052 Holzbau
DIN 18800 T2 Knickspannungsnachweis im Stahlbau
Bezogene Schlankheit: λquerk = lambda/lambdaF
σF = π2 * E / λF2
Bezugsschlankheit lambdaF
reale Knickspannung σkr = κ * σF
plastische Normalkraft NPl
tatsächlich vorhandene Normalkraft ND = γF * N
Nachweis:
- Bezugsschlankheit
- Knicklängen
- Schlankheiten
- bezogene Schlankheiten
- Knickspannungslinien aus DIN 18800
- Abminderungswerte (κ)
- Plastische Normalkraft
- Tragsicherheitsnachweis
Knicklängenbeiwerte über Ersatzsysteme
Druckbehaftete und nicht druckbehaftete Teile des Systems trennen.
Durch eine Drehfeder ersetzen.
Federgesetz: M= cφ* φ
cφ Drehfederkonstante
φ Dtehwinkel
Wegfeder: F = c * w
Bestimmung der Federkonstanten
φ = Verdrehung der Tangente an die Biegelinie.
Tragsicherheitsnachweis gemäß DIN 18800 T2
Spannungstheorie 2. Ordnung
Der Gleichgewichtszustand wird am verformten System ermittelt.
Das Superpositionsprinzip ist nicht gültig.
Nachweise sind stests mit den Bemessungslasten bzw. Bemessungswerten der Widerstände zu führen (design-Werte).
Das System ist mit Vorverformungen zu beaufschlagen (Vorkrümmung, Schiefstellung).
Bestimmung der elastischen Grenzlast
w'' + λ2 * w = -λ2 * wv
DGL 2. Ordnung inhomogenen Typs
Ansatz: w(x)= A * sin(π/l*x)
mit ε = λ * l
A = ε2/(π2-ε2)*wv
elastische Grenzlast
Nki = π2 * E *I /l2
Spannungsnachweis:
Näherung nach Dischinger
MII = MI * (Nki / N + δ) / (Nki/N-1)
Statisch unbestimmte Systeme
Kraftgrößenverfahren
einfach statisch unbestimmte Systeme
Das <b>Grundsystem</b> wird durch Entfernung statischer Größen im Ausgangssystem gewonnen.
Zustand 0 = Grundsystem unter realer Belastung
Ort 1 = Stelle, an der die erste statische Größe entfernt wurde.
δ1,0 Verformung. Der erste Index bezeichnet den Ort der Verformung. Der zweite Index bezeichnet die Ursache der Verformung.
Zustand 1 = Grundsystem unter der Wirkung der ersten statischen Unbekannten.
Resultat: δ1,1
Bestimmuug der Velformungen
δ10
Überlagerung beider Zustände, um das Ausgangssystem zu erhalten (Superpositionsprinzip)
Verträglichkeitsbedingung oder Elastizitätsbedingung:
δ1 = δ10 + x * δ11 = 0
x = statische Unbekannte
Bestimmung der übrigen statischen Größen
M = MO + x * M1
Alternativ kann eine innere statische Größe entfernt werden.
Zweifeldträger