Stand 2000
"Überlassen wir die Physiker, die Mathematiker und die Philosophen sich selber, treiben wir sie endgültig in die Ghettos ihrer Fachgebiete zurück, wo sie hilflos und unbemerkt den Raubzügen der Techniker und der Ideologien ausgeliefert sind; Raubzüge, die immer stattfanden und immer wieder stattfinden." - Friedrich Dürrenmatt
Physikalische Begriffsdefinitionen für Bauingenieure.
Dichte - spezifische Masse
Die spezifische Masse eines Körpers ist das Verhältnis seiner Masse zu seinem Volumen.
Wichte - spezifisches Gewicht
Das spezifische Gewicht eines Körpers ist das Verhältnis seiner Gewichtskraft zu seinem Volumen.
Gewicht
Das Gewicht eines Körpers ist die Kraft, die er erfährt, weil seine Masse der Fallbeschleunigung g ausgesetzt ist.
Kugelvolumen
Bei bekanntem Radius ergibt sich das Volumen einer Kugel nach folgender Beziehung:
VK = 4/3 * π * r3
Elastizitätsmodul
Der Elastizitätsmodul E, auch kurz E-Modul genannt, ist ein Materialparameter, der bestimmt, wie sich ein Körper unter einer Zug- oder Druckkraft in Richtung der Kraft verformt.
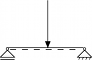
Wenn am oben eingespannten Stab der Länge L am unteren Ende eine senkrecht nach unten gerichtete Zugkraft F angreift, ergibt sich eine Längenänderung. Ist die Kraft nicht zu groß, so wird sich das Material elastisch verformen, d.h., es wird seine ursprüngliche Form wieder annehmen, wenn der Zug entfällt.
Führt man mehrere Versuchsreihen durch, so ergibt sich:
F ∝ ΔL / L * A
A ist in diesem Fall die Querschnittsfläche des Stabes, außerdem wird die Querschnittsänderung vernachlässigt. Nun kann man den E-Modul E als Proportionalitätsfaktor einführen:
[E] = N / μ = Pa
Kompressionsmodul
Analog zum Elastizitätsmodul läßt sich der Kompressionsmodul definieren: Erfahren ein Körper, eine Flüssigkeit oder ein Gas eine Druckerhöhung, ohne daß sie ausweichen können, so rücken ihre Moleküle näher zusammen. Mit anderen Worten: Ihr Volumen verkleinert sich.
Die Größe dieser Kompression ist material- und druckänderungsabhängig. Es läßt sich für die einzelnen Materialien zeigen, daß der Quotient aus der Volumenänderung und dem ursprünglichen Volumen proportional zur negativen Druckänderung ist.
Der Kompressionsmodul K ist der zugehörige Proportionalitätsfaktor.
[K] = Pa = N / μ
Kompressibilität
Die Kompressibilität k eines Materials ist der Kehrwert seines Kompressionsmoduls.
Sie macht anschaulich, wie leicht ein Material zu komprimieren ist: Ist die Kompressibilität groß, so läßt sich das Material mit geringem Druck stark komprimieren.
[k] = 1 / Pa = μ / N
Querkontraktion
Erfährt ein Körper Druck oder Zug und kann sich frei verformen, so verändert sich nicht nur seine Länge, sondern auch seine Dicke. Diese Erscheinung wird als Querkontraktion bezeichnet.
Es läßt sich Für jedes Material zeigen, daß die relative Längenänderung ΔL proportional zur relativen Dickenänderung ΔD ist.
Die Poisson'sche Querkontraktionszahl ist der materialabhängige Proportionalitätsfaktor.
Schubmodul
Erfährt ein einseitig gehaltener Quader eine Kraft, die in der der Einspannfläche gegenüberliegenden Oberfläche angreift, so wird der Quader auf Scherung beansprucht.
Eine solche Kraft kann natürlich auch die vektorielle Komponente einer schräg angreifenden Kraft sein. Es ergibt sich eine Auslenkung x. Die Größe der aufgewendeten Kraft ist proportional zur Auslenkung und zur Grundfläche A des Quaders. Sie ist reziprok proportional zur Höhe h des Quaders, außerdem hängt die Auslenkung vom Material des Quaders ab.
Der Schubmodul G ist der Proportionalitätsfaktor in dieser Beziehung. Er ist ein Materialparameter.
Man kann die Größe der Auslenkung auch über den Winkel beschreiben.
Linearer Ausdehnungskoeffizient
Erwärmt man einen Stab der Länge L0 , so dehnt er sich aus. Die Länge des Stabes ändert sich. Die Längenänderung ist proportional zum Produkt aus der Temperaturdifferenz und der Ausgangslänge.
Als Proportionalitätsfaktor führt man den linearen Längenausdehnungskoeffizienten ein. Die Längenänderung ist die Differenz der von der temperaturabhängigen Länge des Stabes Lt und der Ausgangslänge L0.
Volumenausdehnungskoeffizient
Ein Körper, der aus einem einzigen Material besteht und eine Temperaturzunahme erfährt, dehnt sich in alle Richtungen gleichmäßig aus.Für die drei Raumdimensionen gilt jeweils der lineare Ausdehnungskoeffizient.
Abhängigkeit der Dichte von der Temperatur
Die Dichte eines Körpers ist der Quotient aus seiner Masse und seinem Volumen. Da das Volumen des Körpers von der Temperatur abhängig ist, ist auch seine Dichte temperaturabhängig.
Temperatur
Die absolute Temperatur eines Stoffes ist proportional zur Summe der kinetischen Energien aller seiner Teilchen.
Sind alle Teilchen des Stoffes in Ruhe, so hat der Stoff die absolute Temperatur T = 0 K. Das entspricht einer Temperatur von t = -273 °C.
Es gilt:
[T] = K
Wärme
Um die Temperatur eines Körpers zu erhöhen, muß man ihm Energie zufähren. Unter adiabatischen Bedingungen ist die zugeführte Energiemenge ΔQ proportional zur Temperaturerhähung ΔT.
Die Energiemenge, die benötigt wird um die Temperatur eines Körpers um 1K zu erhöhen, ist proportional zu seiner Masse m und seiner spezifischen Wärmekapazität c. Das Produkt aus m und c ist die Wärmekapazität des Körpers.
Die spezifische Wärmekapazität ist ein Materialparameter, der angibt, wieviel Wärmeenergie benötigt wird, um 1 kg des Materials um 1 K zu erwärmen.
Es gilt:
[c] = J *K-1 *kg-1
[Q] = kg * J * K-1 *kg-1 * K = J
Dampfdruckkurve
Die oben angeführten Betrachtungen gelten nicht mehr, wenn die Temperatur des Mediums sich so verändert, daß der Aggregatzustand des erwärmten Mediums wechselt. Ab einem bestimmten Punkt erwärmt sich das Medium bei weiterer Energiezufuhr nicht mehr. Statt dessen geht ein Teil des Mediums in eine andere Phase äber. Erst wenn sich das Medium vollständig in der neuen Phase befindet, steigt seine Temperatur bei Energiezufuhr weiter an.
Die Menge des Mediums, das die Phase gewechselt hat, ist proportional zur zugeführten Energie. Die zugehörige Proportionalitätskonstante ist die für das Verdampfen die spezifische Verdampfungswärme r. Sie ist ein Materialparameter, der angibt, wieviel Wärmeenergie aufgewendet werden muß, um 1 kg eines Materials zu verdampfen.
Eine Energiezufuhr erhöht den Dampfdruck des Mediums.
Die Menge des verdampften Mediums:
ΔQ = r * m
[r] = kJ * kg-1
Wärmestrom
Der Wärmestrom f ist die Energiemenge ΔQ, die in der Zeit Δt durch ein Bauteil transportiert wird.
Wärmeübergang
Der Wärmeübergangskoeffizient a ist der Wärmestrom in Watt, der bei einer Temperaturdifferenz von 1 K zwischen Medium und Oberfläche auf eine 1 m² große Fläche übertragen wird. Die übertragene Wärmeenergie läßt sich in verschiedene Anteile aufteilen: Einen Anteil, der durch Konvektion, einen Anteil, der durch Wärmeleitung und einen Anteil, der durch Wärmestrahlung übertragen wird.
[a]=W*m-2*K-1
Wärmekonvektion
Wärmekonvektion ist der Transport von Wärmeenergie im Materiestrom.
 Bild 1  Bild 2 |
Ein Beispiel für Wärmekonvektion liefert der folgende Versuch: Die linke Röhre in Bild 1 enthält Wasser, das deutlich kälter ist als das gefärbte Wasser in der rechten Röhre. Das Wasser in beiden Röhren ist wärmer als 4°C. Öffnet man die Ventile in den waagerechten Verbindungsröhrchen, so ergibt sich innerhalb von Sekunden ein neues Bild: Wie in Bild 2 dargestellt, bilden sich innerhalb des Röhrensystems zwei Schichten aus - oben das, spezifisch leichtere, wärmere Wasser, unten das kältere Wasser. Zusammen mit dem Materiestrom des wärmeren Wasser ist auch dessen Wärmeenergie in die linke Röhre transportiert worden. Die Angleichung der Wassertemperaturen durch Wärmeleitung, Strahlung und Diffusion geschieht wesentlich langsamer, so daß in den beiden Schichten zunächst noch Temperaturen gemessen werden, die den Ausgangstemperaturen in den beiden Röhren entsprechen. |
Wärmeleitung
Wärmeleitung ist der Transport von Wärmeenergie durch Schwingungsübertragung zwischen Teilchen.
Wärmestrahlung
Wärmestrahlung ist der Transport von Wärmeenergie durch elektromagnetische Strahlung.
Fiktive Förderhöhe
Das pro Zeiteinheit von einer Pumpe geförderte Volumen eines Mediums ist abhängig von der geodätischen Förderhöhe, von den äußeren Druckverhältnissen und den Energieverlusten durch Reibung und Rohrkrümmung. Um die Pumpenleistung einfach vergleichen zu können, errechnet man eine fiktive Förderhöhe, in die geodätische Förderhöhe, Druckverhältnisse und Energieverluste eingehen. Je größer diese fiktive Förderhöhe ist, desto geringer ist das geförderte Volumen.
Pumpenkennlinie
Für jede Pumpe läßt sich eine Pumpenkennlinie als Diagramm der fiktiven Förderhöhe H über Q, dem geförderten Volumen pro Zeit, darstellen.
Anlagenkennlinie
Ebenso läßt sich für jede Anlage, in der eine Pumpe eingesetzt wird, eine Anlagenkennlinie als Diagramm der fiktiven Förderhöhe über dem geförderten Volumen pro Zeit darstellen.
Arbeitspunkt
Stellt man eine Anlagenkennlinie und eine Pumpenkennlinie in einem Diagramm dar, so ist der Schnittpunkt der beiden Kennlinien der Arbeitspunkt. Der Arbeitspunkt ist der Punkt, an dem das System am wirtschaftlichsten arbeitet.
Weitere Begriffe und Definitionen
Weitere Definitionen zu den folgenden Themen: Elektrik, Elektrische Leistung, Elektrischer Widerstand, Elektromotor, Flüssigkeiten